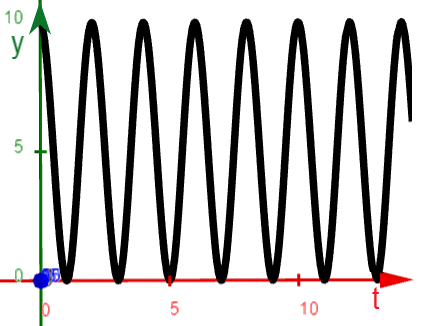
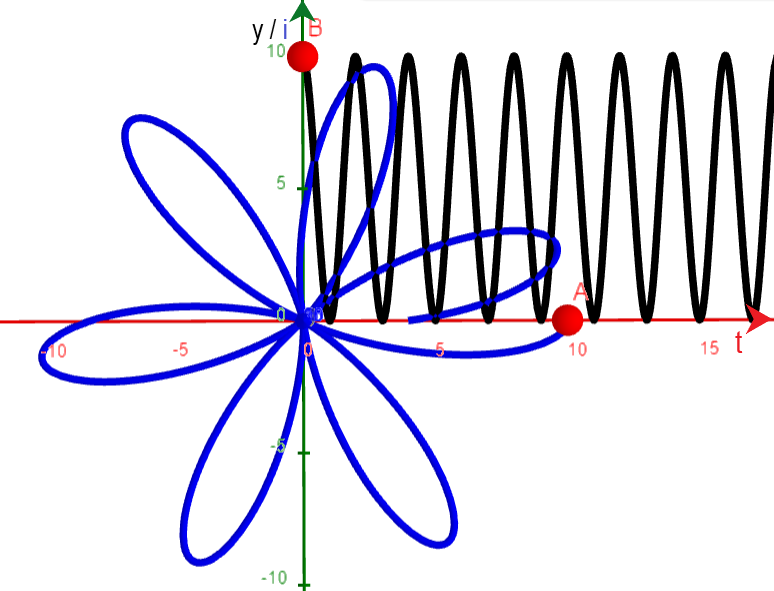
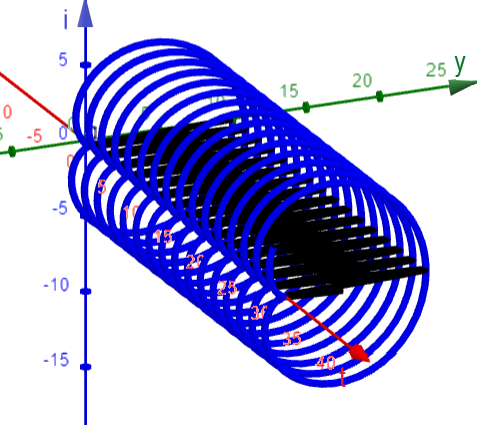
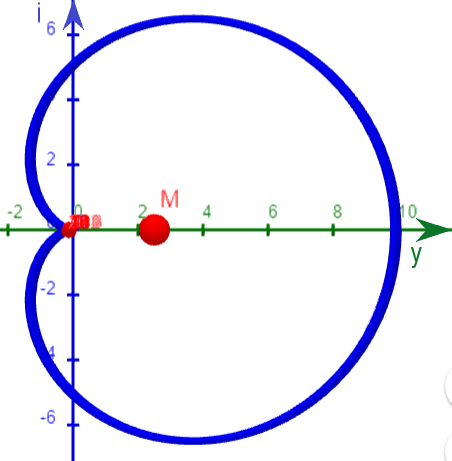
Analytische Methode
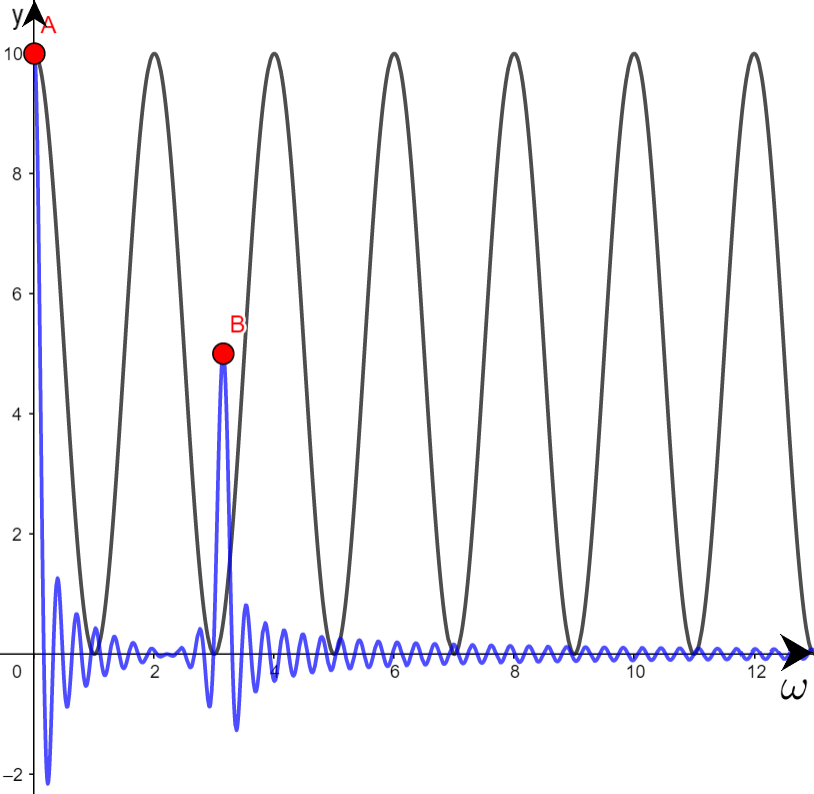
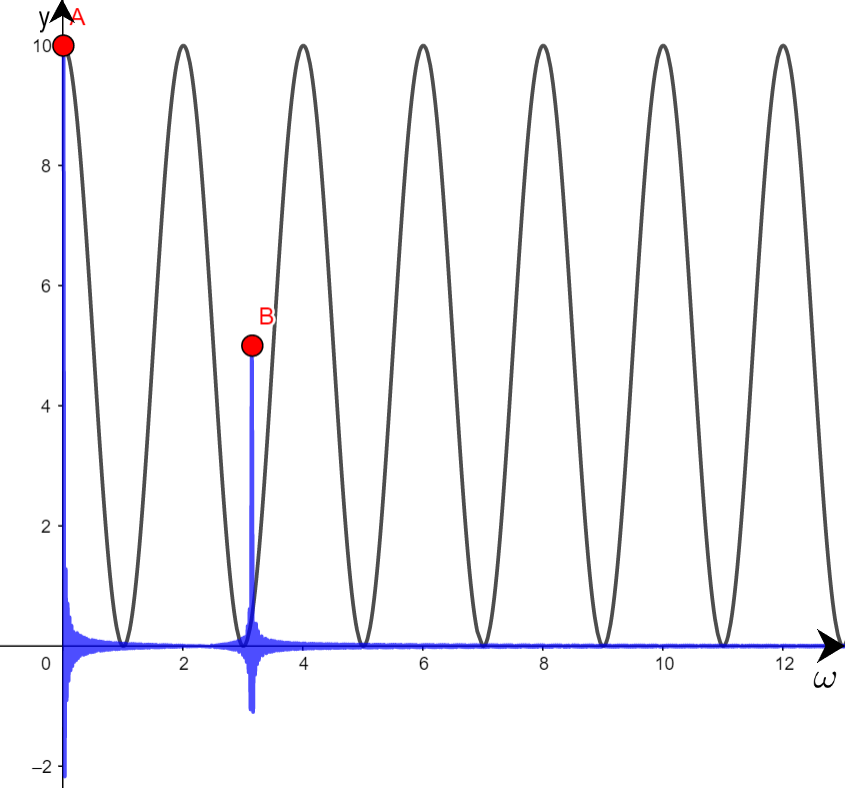
Im Folgenden sieht man geradewegs entlang der Zeitachse. Außerdem wurde ein Massepunkt \(M\) (rot) hinzugefügt. Man erkennt, dass er nicht bei \(0\) liegt, sondern bei \( (2,5;0) \). Normalerweise würde sich der Massepunkt nahe Null befinden, wenn die Frequenz \( \frac{\omega}{2\pi} \) nicht im Signal \( f(t) \) enthalten wäre.
Um die Frequenz "automatisch zu ermitteln", wird das Integral der Funktion \( g(t) \) über die Zeit \( t \) berechnet. Das Integral ist im Prinzip eine Summe und somit kann der Massepunkt als Schwerpunkt der Funktion \( g(t) \) betrachtet werden.
Um die richtige Amplitude zu bestimmen, wird die Funktion \( g(t) \) mit \( \frac{2}{x} \) multipliziert. (Allgemein: \( \frac{2}{x_1-x_2} \) ist die Länge des Intervalls, in dem die Funktion \( f(t) \) definiert ist.)
\[
\begin{align*}
\int_{0}^{x}f(t)\cdot e^{-i\omega t} &= \int_{0}^{x}(5\cdot (\cos(\pi t)+1)) e^{-i \omega t}dt \\
&= 5\cdot \int_{0}^{x} (\cos(\pi t)+1)\cdot e^{-i \omega t}dt \\
&= 5\cdot \int_{0}^{x} \left(\frac{e^{i\pi t}+e^{-i\pi t}}{2}+1\right)\cdot e^{-i \omega t}dt \\
&= 5\cdot \int_{0}^{x} \frac{1}{2}\left(e^{i\pi t}+e^{-i\pi t}+2\right)\cdot e^{-i \omega t}dt \\
&= \frac{5}{2} \int_{0}^{x} \left(e^{-i t(\pi -\omega)} + e^{-i t(\pi +\omega)} + 2e^{-i \omega t}\right) dt \\
&= \frac{5}{2} \left[ \frac{e^{-i t(\pi -\omega)}}{i(\pi - \omega)} + \frac{e^{-i t(\pi +\omega)}}{-i(\pi + \omega)} + \frac{2e^{-i \omega t}}{-i \omega} \right]_{0}^{x} \\
&= \frac{5}{2} \left[ \left( \frac{e^{-i t(\pi -\omega)}}{\omega - \pi} + \frac{e^{-i t(\pi +\omega)}}{\pi + \omega} + \frac{2e^{-i \omega t}}{ \omega} \right) \frac{1}{-i} \right]_{0}^{x} \\
&= \frac{5}{-2i} \left[ \left( \frac{e^{-i x(\pi -\omega)}}{\omega - \pi} + \frac{e^{-i x(\pi +\omega)}}{\pi + \omega} + \frac{2e^{-i \omega x}}{ \omega} \right) - \left( \frac{1}{\omega - \pi} + \frac{1}{\omega + \pi} + \frac{2}{\omega} \right) \right] \\
&= \frac{5}{-2i} \left[ \left( \frac{e^{-i x(\pi -\omega)}}{\omega - \pi} + \frac{e^{-i x(\pi +\omega)}}{\pi + \omega} + \frac{2e^{-i \omega x}}{ \omega} \right) - \left( \frac{1}{\omega - \pi} + \frac{1}{\omega + \pi} + \frac{2}{\omega} \right) \right] \\
F(\omega) &= \frac{5}{-2i} \left( \frac{e^{-i x(\pi -\omega)}}{\omega - \pi} + \frac{e^{-i x(\pi +\omega)}}{\pi + \omega} + \frac{2e^{-i \omega x}}{ \omega} - \frac{4\omega^2 - 2\pi^2}{\omega^3 - \omega \pi^2} \right) \\
F(\omega) \cdot \frac{2}{x} &= \frac{10}{-2i \cdot x} \left( \frac{e^{-i x(\pi -\omega)}}{\omega - \pi} + \frac{e^{-i x(\pi +\omega)}}{\pi + \omega} + \frac{2e^{-i \omega x}}{ \omega} - \frac{4\omega^2 - 2\pi^2}{\omega^3 - \omega \pi^2} \right)
\end{align*}
\]
Anmerkung: \( \cos(x) = \frac{e^{ix}+e^{-ix}}{2} \) und \( \sin(x) = \frac{e^{ix}-e^{-ix}}{2i} \)
Die erste Abbildung zeigt die Funktion \( F(\omega) \) mit \( x = 20 \) und die zweite mit \( x = 200 \).